Project 2

Part 1 - Objective

The objective of this project is to analyze the data set provided and develop a model that would help predict firm demand. Predicting firm demand will enable the firm plan its marketing and sales goals, which will ultimately lead to manage its finance as well as manufacturing operations in an effective and more efficient way.

The basic mathematical equation that will be used is:

Firm Demand (FD) = Total Industry Demand (TID)*Market Share(MS) = TID *RD/N

The key variables of interest that will be used to develop the models are outlined below:

TID  = Total Industry Demand - useful in determining overall market growth
AFD = Average Firm Demand = (TID/N) where N denotes the number of firms in the industry (10)
FD  = Firm Demand
RD = Relative Demand- shows how the firm's demand compares with the AFD. RD=FD/AFD
MS = Market Share of the firm = RD/N
PREL = Relative Price - shows the firm's price relative to the industry's average price
AREL = Relative Advertising - shows the firm's advertising cost relative to industry's average advertising expenditures
RD1 = Last Quarter's relative demand-it is a measure of brand loyalty

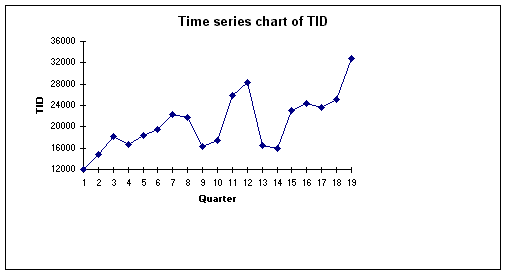
The provided dataset will be used to develop models that will help in estimating TID & RD.

TID as a function of time as well as Average Price/Average Advertising
These are some thoughts that came to my mind before looking at the dataset in question: TID is likely to vary with time. During the market growth stages, TID may increase. However, it is likely that after the market saturates TID may decrease with time. TID is likely to be impacted by average price of goods sold. By theory of demand, as the average price increases, the demand decreases. As advertising expenditures increase, TID is bound to increase because of increased brand awareness among consumers.

RD as a function of PREL, AREL and RD1
These are some thoughts that came to my mind before looking at the dataset in question : Clearly as PREL increases, by theory of demand, it is likely that RD for the firm's product is bound to decrease. Likewise, when PREL decreases, it is likely RD for the firm's product is bound to increase. As AREL increases, it is likely that brand awareness for the firm's product increases causing the RD to increase. Likewise, as AREL decreases, it is indicative of the fact that the firm is spending less on advertising than its competitors and hence RD also decreases. RD1 or last quarter's relative demand is a measure of existing brand loyalty on the firm's product. It is bound to influence RD values.
 

Part 2 - Description of Variables

TID Variables

Total Industry Demand (TID) - Trend Analysis

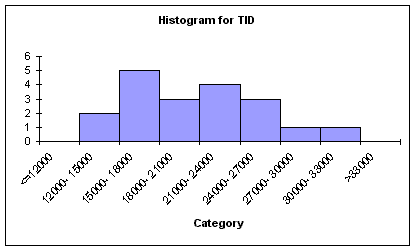
As seen from the above histogram, TID is mainly distributed in the $15000 to $30000 range.

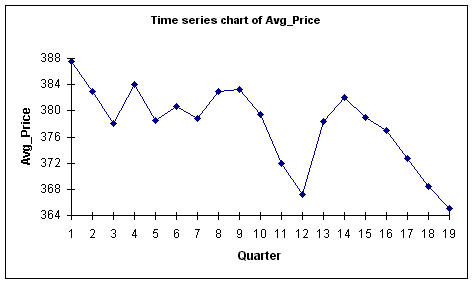
Total Industry Demand(TID) - Summary Measures

Average Price - Trend Analysis

As seen from the above chart, Average Price  has decreased consistently for the most part. There have been quarters where the Average Price has increased sporadically.

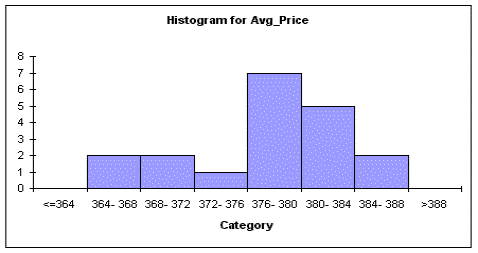
As seen from the above histogram, Average Price  is mainly distributed in the $376 to $388 range.

Average Price - Summary Measures

Average Advertising Expenditures - Trend Analysis

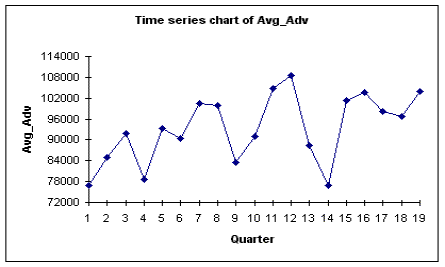
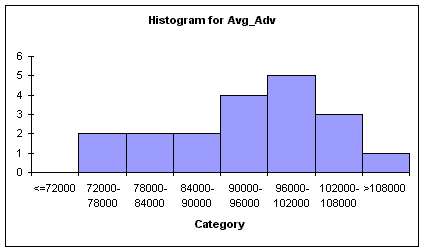
Average Advertising - Summary Measures

The charts above indicate that the mean Average Advertising expenditure is $93,326 with a standard deviation for the dataset being $9828. The line graph shows that there has been a slight increase over time with several sharp spikes (dips) in the average advertising expenditures. The maximum value for the dataset is $108,570 and occurs in Q12 while the minimum value for the dataset is $76,800 and occurs in Q1.

Correlation Matrix of TID, Average Price, Average Advertising and Quarter

The table below outlines the correlation matrix of the variables discussed above. 

Based on the correlation coefficients, the following conclusions can be made :

1. There is a strong correlation between TID as well as Average Price or Average Advertising expenditures. TID is fairly correlated with the quarter (time).
2. Average Price is strongly correlated with the quarter (time).
3. Average Advertising Expenditure is strongly correlated with the Average Price.

Based on the above conclusions, it makes sense to perform regression analysis using the following variables :

• TID and Time
• TID, Avg.Price (AP) and Avg.Advertising (AA)

RD Variables

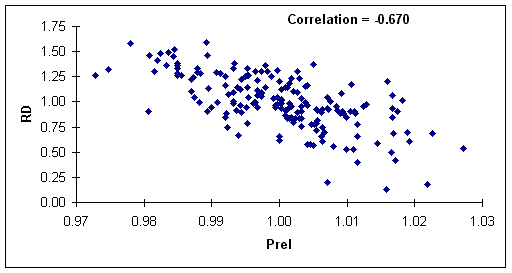
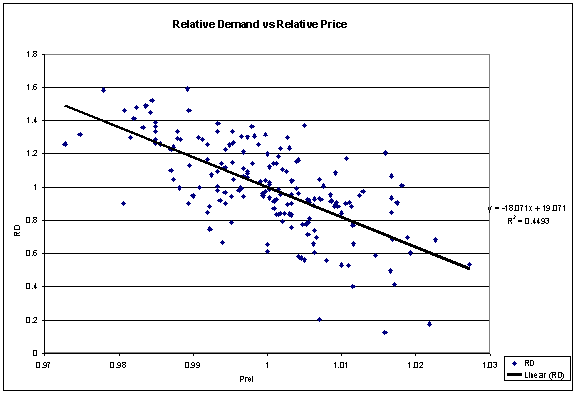
Please refer to Part 1 for description of RD, PREL, AREL & RD1 as well as their significance.

Scatter Plot between RD and PREL

From the scatterplot above, it is obvious that there is a strong inverse correlation between RD & PREL. This was my guess even prior to looking at the dataset. By theory of demand, as price increases demand deceases and vice versa. This RD versus PREL scatterplot just confirms the theory of demand.

 Scatter Plot between RD and AREL

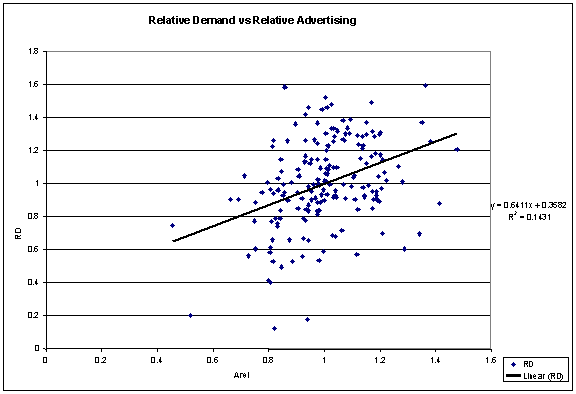
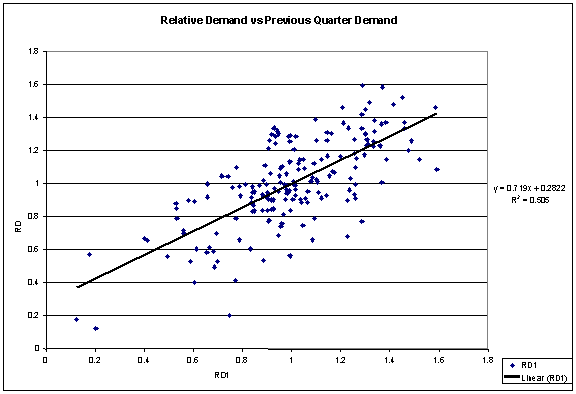
The above scatterplot above indicates that RD & AREL are not strongly correlated. Therefore, increase in advertising expenditures does not directly influence the relative demand for the firm's product.

Scatter Plot between RD and RD1

The above scatterplot indicates that RD and RD1 are strongly correlated. This is suggestive of the fact that customers tend to be brand loyal and is also one of the reasons why advertising is not causing significant influence on customers who might be loyal to existing brands.

Scatter Plot between RD and PREL

Since PREL and RD1 are weakly correlated, it would actually make sense RD as the response variable and PREL as well as RD1 as the predictor variables for performing the regression analysis.

Part 3 - Mathematical Modeling:

Regression Analysis to estimate TID using Quarter (time) as independent variable

The following information was obtained using the dataset provided.

The p-value for the independent variable is 0.001 which is indicative of the fact that the probability of a type 1 error is very low and hence there is a likely relationship between the variables under study.

Based on the data above, the model for TID is :

TID = 645.9825Quarter+14218.0702 

The R² figure indicates that only 48% of the variance in TID is explained by this model. 

Regression Analysis to Estimate TID Using Quarter, AvgPrice and AvgAdvertising as Predictors

The following information was obtained using the dataset provided :

Based on the data above, the model for TID is :

TID = 130249.2813+132.2283Quarter-358.6135(Avg.Price)+0.2634(Avg.Advertising)

An R2 value of 90.69 indicates that the model explains approximately 91% of the variance in TID value. The p-values for Average Price and Average Advertising are 0.0102 and 0.0008 respectively. The adjusted R2 value is 88.83%.

Recommended Model for Estimating TID

Each model has its own merits. The first model is just a function of quarter and hence is easier to measure though it is less predictive as compared to the second model. The second model which is a function of quarter, Average Price and Average Advertising is obviously more difficult to measure because of the fact that three variables are needed to estimate TID. However, due the high values of R2 as well as adjusted R2 values of the latter model, the latter model is the recommended choice for estimating TID in this problem.

Regression Analysis to Estimate RD Using PREL, AREL and RD1 as Predictors

Based on the data above, the model for RD is :

RD = 16.13-16.44PREL+0.7796AREL+0.5334RD1

An R Square value of 95.75%  indicates that the model explains approximately 96% of the variance in RD value.  The t-values and p-values of coefficients are summarized in the above table.

FD Model:

As discussed earlier, the firm demand is described by the equation below:

Firm Demand(FD) = Total Industry Demand(TID)*Market Share(MS) = TID *RD/N

Since optimal models for estimating TID and RD have been developed, arriving at a model for FD  is just a matter of plugging in values for TID and RD in the above equation .Therefore,

FD = TID*RD/N

       where TID = 130249.2813+132.2283Quarter-358.6135   (Avg.Price)+0.2634(Avg.Advertising)
   and   RD  = 16.13-16.44PREL+0.7796AREL+0.5334RD1

Conclusions

Since we have developed models for estimating TID, RD and FD, it should be fairly easy transform this mathematical model into a spreadsheet model. Spreadsheet models are better than mathematical models because they provide instant feedback and prevent the end user from worrying about low level mathematical details. So, in effect a Decision Support System (DSS)  has been developed to help estimate Firm Demand which would in turn facilitate the firm to plan production schedules, manufacturing requirements, project financial revenues, estimate costs and make decisions on pricing, advertising, budgets etc.